
1. 原码、反码和补码
首先我们知道,在计算机中,所有数都是以二进制存在,也就是0和1的组合。
但是通过研究二进制,人们发现了二进制并不能很好的和十进制对应起来。首先十进制中有正数和负数,而二进制中的负号-该如何表示呢?有人想到用二进制的最高位表示,此位为0则表示正数,1表示这个数为负数。
举个例子:
1的二进制为0001,那么-1的二进制就是1001。
但是直接这么表示就会出现刚才提到的对应问题。
例如如果1和-1直接相加,则1 + (-1) = 0,十进制是没有问题的。而二进制表示为0001 + 1001 = 1010 != 0,所以不能直接使用这种方式做运算。而这种直接用最高位表示符号位,其他位表示数字的编码形式称为原码。
原码不能解决这个问题,于是又出现了反码,反码是当这个数为负数时,原码除符号位外其他位取反。1001(-1)(原码)取反后为1110。
继续进行刚才的计算,这次使用反码: (反码)0001 (1) + 1110 (-1) = 1111 。由于1111最高位为1,是负数,所以再次取反之后才是其真实值,取反后为1000,也就是-0。
这能满足条件了,但是美中不足的是,0带了负号。唯一的问题其实就出现在0这个特殊的数值上。 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的。 而且会有0000原和1000原两个编码表示0。怎么办呢?
人们又想出了补码,它的定义是反码加1。-1的补码是 1111,以上的运算用补码表示就是0001 (1) + 1111 (-1) = 0000 = 0。神奇的发现,这个式子完美契合了十进制加法!
同时我们留出了1000,可以用它表示-8
(-1) + (-7) = (补码) 1111 + 1001 = 1000 = -8。注意,由于此处的-8使用了之前-0的补码来表示,所以-8没有没有原码和反码表示(针对的四位,如果是八位,则没有原码和反码的是-128,依次类推)。
使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么4位二进制, 使用原码或反码表示的范围为[-7, +7], 而使用补码表示的范围为[-8, 7].
推广到k位:在处理k位的有符号数时,用二进制补码的形式表示负整数-n(1 $\le$ n $\le$ $2^k - 1$), 则补码的二进制值为$2^k - n$ 。非负整数p(0 $\le$ p $\le$ $2^{k - 1} - 1$),只是简单的用k位二进制数表示p的值。因此对于给定的k位,我们可以通过二进制补码表示$-2^{k - 1}$到$2^{k - 1} - 1$的值。
总结
为了使数字在计算机中运算不出错,出现了原码,反码和补码。原码就是一个数的二进制表示,其中最高位为符号位,表示其正负。
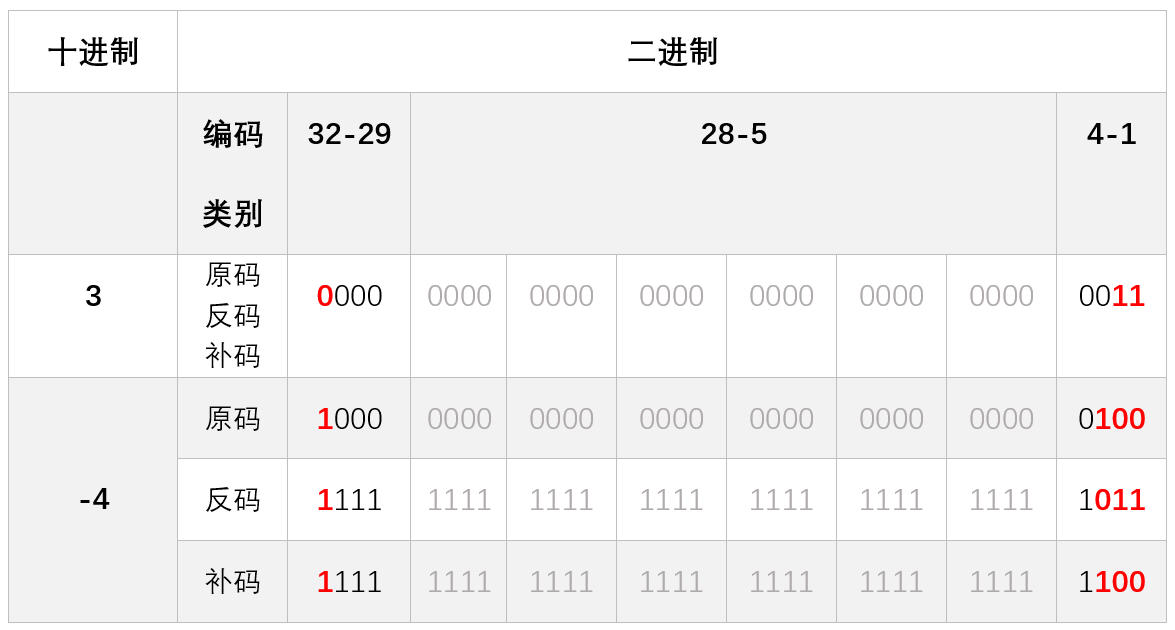
原码,反码和补码运算对比。

这就是简单的要用反码和补码的原因。
2. 大数溢出问题
int类型在32位系统中占4个字节、32bit,补码表示的的数据范围为:
[10000000 00000000 00000000 00000000] ~ [01111111 11111111 11111111 11111111]
[−231,231−1]
[-2147483648, 2147483647]
在java中表示为:
[Integer.MIN_VALUE, Integer.MAX_VALUE]
与byte类型的表示一样,由于负数比正数多表示了一个数字。对下限取相反数后的数值会超过上限值,溢出到下限,因此下限的相反数与下限相等;对上限去相反数的数值为负值,该负值比下限的负值大1,在可以表示的范围内,因此上限的相反数是上限直接取负值。也就是
1 | int a = Integer.MIN_VALUE; |